에라토스테네스의 체 개념 및 구현

Intro

이 글은 에라토스테네스의 체 개념과 구현에 대해서 다룹니다.

---

에라토스테네스의 체 개념 및 특징

에라토스테네스의 체 개념

에라토스테네스의 체는 수학자 에라토스테네스의 이름을 딴 알고리즘으로, 소수를 대량으로 빠르고 정확하게 구하는 소수판별 알고리즘이다.

특징

에라토스테네스의 체로 2부터 N까지의 수 중에서소수를 판별하는 과정은 다음과 같다.

1. 2부터 N까지의 범위를 저장하는 배열을 선언한다.
2. 배열 범위 내에 있는 2의 배수를 모두 지운다.(혹은 특정 표시를 한다.)
3. 그 다음에 3을 제외한 3의 배수를 모두 지운다.
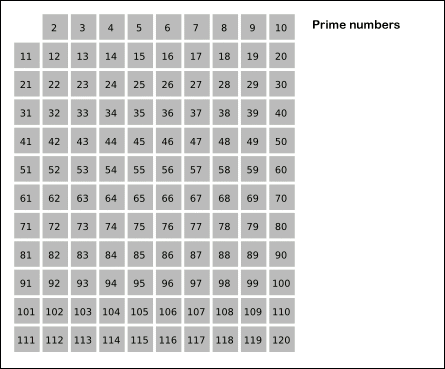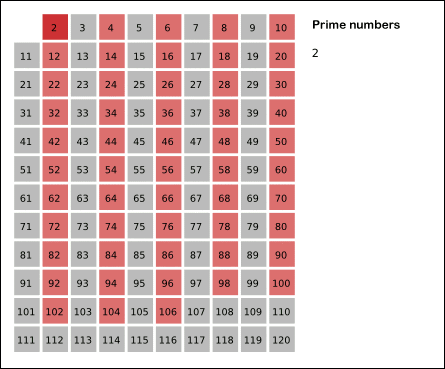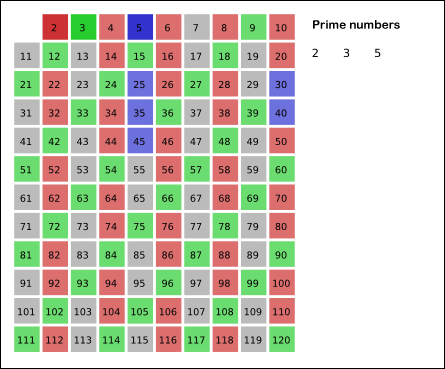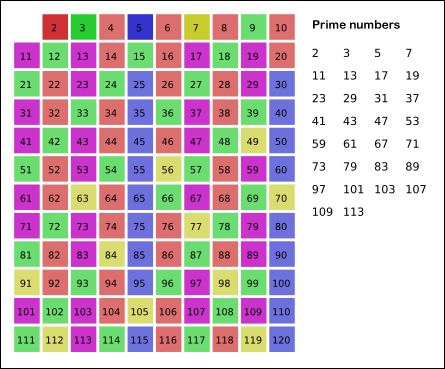
4. 이 과정을 N의 제곱근까지 반복한다. (N 제곱근 이상의 숫자를 곱하면 N을 벗어나기 때문이다.

이 과정이 종료되면 배열에는 소수만 남게 된다.

에라토스테네스의 체는 O(NloglogN)의 시간복잡도를 가진다. 하지만 N의 크기만큼 리스트를 할당해야 하기 때문에 메모리가 많이 필요하다는 단점이 존재한다.

---

에라토스테네스의 체 구현(백준 9020 골드바흐의 추측)

에라토스테네스의 체를 구현해 볼만한 문제로는 백준 9020 골드바흐의 추측이 있다.

구현 코드

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define SIZE 10001

void Eratosthenes(int arr[]){
    
    for (int i = 2; i <= sqrt(SIZE); i++){
        if (arr[i] == 0){
            for (int j = 2; i * j < SIZE; j++){ // i * j 가 중요합니다!!!!
                arr[i*j] = 1;
            }
        }
    }
}


int main(void){
    
    int N;
    scanf("%d", &N);
    int* prime = (int*)calloc(SIZE, sizeof(int)); // 0으로 초기화
    Eratosthenes(prime);
    
    for(int i = 0; i < N; i++){
        int num;
        scanf("%d", &num);
        int left = num / 2;
        int right = num / 2;
        for (int j = 0; j < num; j++){
            if(left+right == num && prime[left] == 0 && prime[right] == 0){
                printf("%d %d\n", left, right);
                break;
            }
            else{
                left--;
                right++;
            }
        }
    }
    
    
}