이진 탐색 트리(Binary Search Tree) 개념 및 구현
Intro
이 글에서는 이진 탐색 트리의 개념과 특징 및 구현 과정에 대해서 다룹니다.
이진 탐색 트리 개념 및 특징
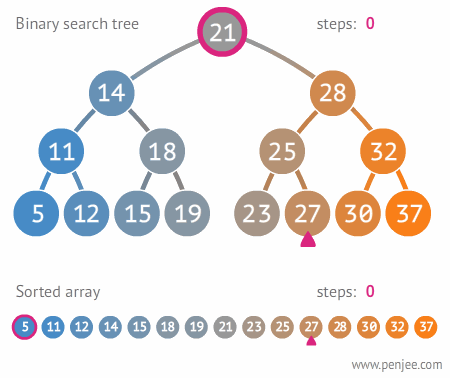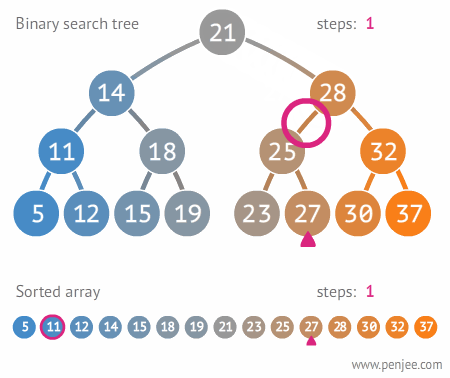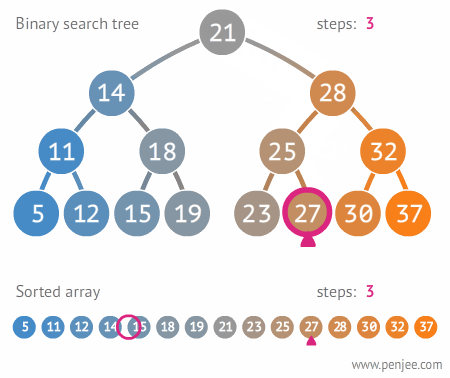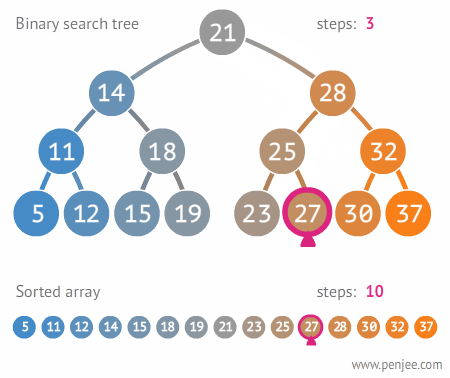
이진 탐색 트리 개념
이진 탐색 트리(Binary Search Tree)는 ‘이진 탐색’을 위한 트리이자, 탐색을 위한 ‘이진 트리’이다. 즉 ‘이진 탐색’을 위한 ‘이진 트리’ 라고 말할 수 있다.
이진 탐색 트리 특징
이진 탐색 알고리즘은 배열에서만 사용이 가능한 알고리즘이기 때문에, ‘중앙 요소‘를 파악하기 어려운 링크드 리스트와 같은 자료 구조에서는 이진 탐색 트리를 사용할 수밖에 없다.
이진 탐색 트리의 중요한 원칙은 “왼쪽 자식 노드는 부모 노드보다 작고, 오른쪽 자식 노드는 부모 노드 보다 크다“는 것이다. 이 원칙을 통해서 이진 탐색 트리는 범위를 좁혀 가면서 탐색을 진행을 할 수 있다.
위의 예시를 통해 알 수 있듯이 27을 찾는다고 했을 때, 해당 이진 트리에서는 3단계 만에 27을 찾아내지만, 일반적인 링크드 리스트에서는(순차 탐색을 할 수밖에 없기에) 27을 찾는데 10단계가 소요된다.
단점
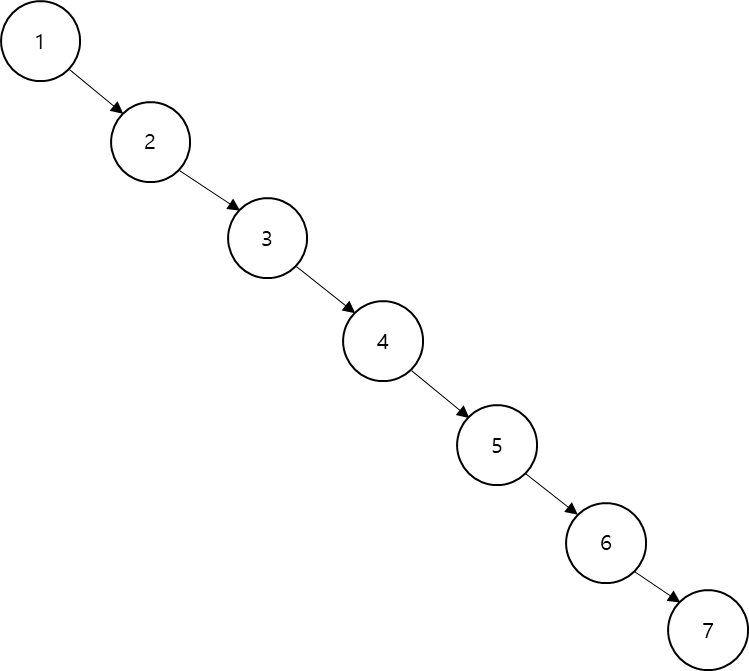
이진 탐색 트리는 동적으로 크기가 증가하는 데이터에서도 매우 좋은 성능의 검색 성능을 가지지만, 기형적으로 크기가 증가하는 데이터에서는 검색 효율이 극단적으로 떨어진다는 단점을 가지고 있다. 이 문제를 해결하기 위해서는 트리의 구조를 균형적으로 유지해야 한다. 이 부분에 관해서는 나중에 포스팅할 레드 블랙 트리 구조를 참고하면 좋다.
이진 탐색 트리 구현
이러한 이진 탐색 트리를 구현하기 위해서 중요한 연산은 바로 노드 삽입 연산과 노드 삭제 연산이다.
트리의 구조 상, 자식 노드를 포함하고 있을 수 있기 때문에 노드를 어떻게 삽입할지, 어떻게 삭제할 지에 대한 방법론적 고찰이 요구되기 때문이다.
이진 탐색 트리의 자세한 구현 과정은 아래와 같다.
1. 노드 삽입 연산
// 노드 삽입 연산
void BST_InsertNode(BSTNode* Tree, BSTNode* Child){
if (Tree->data < Child->data){ // 대소 비교를 통해 자식 노드보다 값이 작으면(자식 노드가 더 크면)
if (Tree->Right == NULL){
Tree->Right = Child; // 오른쪽 노드가 비어있다면 자식노드 넣기
}
else{
BST_InsertNode(Tree->Right, Child); // 비어있는게 아니라면 오른쪽 노드의 자식노드로 넣기.
}
}
else if (Tree->data > Child->data){ // 자식 노드가 더 작으면
if (Tree->Left == NULL){
Tree->Left = Child; // 왼쪽 노드가 비어있다면 자식 노드 넣기
}
else{
BST_InsertNode(Tree->Left, Child); // 비어있는게 아니라면 트리의 왼쪽 노드의 자식노드로 넣기
}
}
}
기준 노드보다 작은 값은 왼쪽에, 큰 값은 오른쪽에 할당되는 이진 탐색 트리의 특성을 고려해서 노드를 삽입할 때 대소 비교를 통해 위치를 할당하는 방법을 고려해야 한다. 그리고 알맞은 위치를 찾아가기 위한 반복 과정은 재귀를 통해서 구현을 한다.
2. 노드 삭제 연산
//노드 삭제 연산 : 자식 노드가 없는 경우. 자식 노드가 하나만 있는 경우, 자식 노드가 두 개 있는 경우로 생각!!
BSTNode* BST_RemoveNode(BSTNode* Tree, BSTNode* Parent, int target){
BSTNode* Removed = NULL;
if (Tree == NULL){
return NULL;
}
if (Tree->data > target){ //헤당 노드의 데이터가 삭제할 값보다 크면,
Removed = BST_RemoveNode(Tree->Left, Tree, target); //Removed에 해당 노드의 왼쪽 노드 할당.
}
else if (Tree->data < target){ // 해딩 노드의 데이터가 삭제할 값보다 작다면,
Removed = BST_RemoveNode(Tree->Right, Tree, target); // Removed에 해당 노드의 오른쪽 노드 할당
}
else{ // 만약 삭제할 노드와 같다면
Removed = Tree; // Removed에 해당 노드 할당
if (Tree->Left == NULL && Tree->Right == NULL){ // 해당 노드의 왼쪽 노드와 오른쪽 노드 모두 없으면
if (Parent->Left == Tree){ // 그리고 부모 노드의 왼쪽 노드가 해당 노드라면,
Parent->Left = NULL; // 부모 노드의 왼쪽 노드를 NULL로 함으로써, 해당 노드 제거
}
else{ //아니라면
Parent->Right = NULL; //부모 노드의 오른쪽 노드를 NULL로 한다.
}
}
else{ // 해당 노드의 왼쪽 노드와 오른 쪽 노드 모두 없는게 아니라면,
if (Tree->Left != NULL && Tree->Right != NULL){ // 만약 왼쪽 오른쪽 노드 모두 NULL이 아니라면(자식 노드가 두 개 다 있다면)
BSTNode* MinNode = BST_SearchMinNode(Tree->Right); // MinNode에 최소값 할당(삭제할 노드보다 큰 값 중에서 가장 작은 값)
MinNode = BST_RemoveNode(Tree, NULL, MinNode->data); // MnNode에 지울 최소값 노드 주소 할당(아직 메모리 상에 지워지지 않음)
Tree->data = MinNode->data; //Tree의 data에 최소값 저장
}
else{ // 만약 왼쪽 오른쪽 노드 모두 NULL이 아닌게 아니라면(자식 노드가 하나만 있다면)
BSTNode* Temp = NULL; // 임시로 저장할 Temp 노드 선언
if (Tree->Left != NULL){ // Tree의 왼쪽 노드가 NULL이 아니라면
Temp = Tree->Left; // Temp에 Tree의 왼쪽 노드 할당
}
else{ // Tree의 왼쪽 노드가 NULL이라면
Temp = Tree->Right; // Temp에 Tree의 오른쪽 노드 값 할당
}
if (Parent->Left == Tree){
Parent->Left = Temp;
}
else{
Parent->Right = Temp;
}
}
}
}
return Removed;
}
노드 삭제 시에는 단순히 해당 노드를 삭제하는 것 뿐만 아니라, 삭제된 노드와 연결된 자식 노드를 새롭게 연결해야 하는 방안도 고려를 해야 한다.
이를 위해서 먼저 삭제할 노드에게 자식 노드가 없을 때, 자식 노드가 하나만 있을 때, 자식 노드가 두 개 다 있을 때를 각각 고려해서 코드를 작성해야 한다.
삭제할 노드에 자식 노드가 두 개 다 있을 경우, 삭제할 노드의 위치에 새로운 값이 할당 되어야 한다. 바로 삭제할 노드의 자식 노드 중에서 최소값을 찾아서 삭제할 노드의 위치에 할당을 하는 것이다. 그런데 무조건 최소값을 찾기 보다는 삭제한 노드 바로 다음으로 큰 최소값을 찾아야 하므로 삭제할 노드의 오른쪽 방향의 자식 노드로 건너서 최소값 탐색을 진행해야 한다.
위에서 언급한 연산을 반영한 전체 구현 코드는 아래와 같다.
전체 구현 코드
이진 탐색 트리 전체 구현 코드 접기/펼치기
#include <stdio.h>
#include <stdlib.h>
// 노드 선언
typedef struct tagBSTNode{
struct tagBSTNode* Left;
struct tagBSTNode* Right;
int data;
} BSTNode;
BSTNode* BST_CreateNode(int newdata);
void BST_DestroyNode(BSTNode* Node);
BSTNode* BST_SearchMinNode(BSTNode* Tree);
BSTNode* BST_SearchNode(BSTNode* Tree, int target);
void BST_InsertNode(BSTNode* Tree, BSTNode* Child);
BSTNode* BST_RemoveNode(BSTNode* Tree, BSTNode* Parent, int target);
void BST_InorderPrintTree(BSTNode* Node);
void PrintSearchResult(int SearchTarget, BSTNode* Result);
BSTNode* BST_CreateNode(int newdata){
BSTNode* NewNode = (BSTNode*)malloc(sizeof(BSTNode));
NewNode->Left = NULL;
NewNode->Right = NULL;
NewNode->data = newdata;
return NewNode;
}
// 노드 삭제
void BST_DestroyNode(BSTNode* Node){
free(Node);
}
// 트리 삭제
void BST_DestroyTree(BSTNode* Tree){
if (Tree->Right != NULL){
BST_DestroyTree(Tree->Right); // 노드 없앨때는 오른쪽부터
}
if (Tree->Left != NULL){
BST_DestroyTree(Tree->Left);
}
Tree->Left = NULL;
Tree->Right = NULL;
BST_DestroyNode(Tree);
}
// 이진 탐색
BSTNode* BST_SearchNode(BSTNode* Tree, int target){
if (Tree == NULL){
return NULL;
}
if (Tree->data == target){
return Tree;
}
else if (Tree->data > target){
return BST_SearchNode(Tree->Left, target); // 타겟 노드값이 현재 노드보다 작은 경우
}
else{
return BST_SearchNode(Tree->Right, target); // 타겟 노드값이 현재 노드보다 큰 경우
}
}
// 최소값 찾기
BSTNode* BST_SearchMinNode(BSTNode* Tree){
if (Tree == NULL){
return NULL;
}
if (Tree->Left == NULL){
return Tree;
}
else{
return BST_SearchMinNode(Tree->Left); //제일 최소값은 왼쪽 방향 노드 끝에 저장된다.
}
}
// 노드 삽입 연산
void BST_InsertNode(BSTNode* Tree, BSTNode* Child){
if (Tree->data < Child->data){ // 대소 비교를 통해 자식 노드보다 값이 작으면(자식 노드가 더 크면)
if (Tree->Right == NULL){
Tree->Right = Child; // 오른쪽 노드가 비어있다면 자식노드 넣기
}
else{
BST_InsertNode(Tree->Right, Child); // 비어있는게 아니라면 오른쪽 노드의 자식노드로 넣기.
}
}
else if (Tree->data > Child->data){ // 자식 노드가 더 작으면
if (Tree->Left == NULL){
Tree->Left = Child; // 왼쪽 노드가 비어있다면 자식 노드 넣기
}
else{
BST_InsertNode(Tree->Left, Child); // 비어있는게 아니라면 트리의 왼쪽 노드의 자식노드로 넣기
}
}
}
//노드 삭제 연산 : 자식 노드가 없는 경우. 자식 노드가 하나만 있는 경우, 자식 노드가 두 개 있는 경우로 생각!!
BSTNode* BST_RemoveNode(BSTNode* Tree, BSTNode* Parent, int target){
BSTNode* Removed = NULL;
if (Tree == NULL){
return NULL;
}
if (Tree->data > target){ //헤당 노드의 데이터가 삭제할 값보다 크면,
Removed = BST_RemoveNode(Tree->Left, Tree, target); //Removed에 해당 노드의 왼쪽 노드 할당.
}
else if (Tree->data < target){ // 해딩 노드의 데이터가 삭제할 값보다 작다면,
Removed = BST_RemoveNode(Tree->Right, Tree, target); // Removed에 해당 노드의 오른쪽 노드 할당
}
else{ // 만약 삭제할 노드와 같다면
Removed = Tree; // Removed에 해당 노드 할당
if (Tree->Left == NULL && Tree->Right == NULL){ // 해당 노드의 왼쪽 노드와 오른쪽 노드 모두 없으면
if (Parent->Left == Tree){ // 그리고 부모 노드의 왼쪽 노드가 해당 노드라면,
Parent->Left = NULL; // 부모 노드의 왼쪽 노드를 NULL로 함으로써, 해당 노드 제거
}
else{ //아니라면
Parent->Right = NULL; //부모 노드의 오른쪽 노드를 NULL로 한다.
}
}
else{ // 해당 노드의 왼쪽 노드와 오른 쪽 노드 모두 없는게 아니라면,
if (Tree->Left != NULL && Tree->Right != NULL){ // 만약 왼쪽 오른쪽 노드 모두 NULL이 아니라면(자식노드가 두개 다 있다면)
BSTNode* MinNode = BST_SearchMinNode(Tree->Right); // MinNode에 최소값 할당(삭제할 노드보다 큰 값 중에서 가장 작은 값)
MinNode = BST_RemoveNode(Tree, NULL, MinNode->data); // MnNode에 지울 최소값 노드 주소 할당(아직 메모리 상에 지워지지 않음)
Tree->data = MinNode->data; //Tree의 data에 최소값 저장
}
else{ // 만약 왼쪽 오른쪽 노드 모두 NULL이 아닌게 아니라면(자식 노드가 하나만 있다면)
BSTNode* Temp = NULL; // 임시로 저장할 Temp 노드 선언
if (Tree->Left != NULL){ // Tree의 왼쪽 노드가 NULL이 아니라면
Temp = Tree->Left; // Temp에 Tree의 왼쪽 노드 할당
}
else{ // Tree의 왼쪽 노드가 NULL이라면
Temp = Tree->Right; // Temp에 Tree의 오른쪽 노드 값 할당
}
if (Parent->Left == Tree){
Parent->Left = Temp;
}
else{
Parent->Right = Temp;
}
}
}
}
return Removed;
}
void BST_InorderPrintTree(BSTNode* Node){
if(Node == NULL){
return;
}
BST_InorderPrintTree(Node->Left);
printf("%d", Node->data);
BST_InorderPrintTree(Node->Right);
}
void PrintSearchResult(int SearchTarget, BSTNode* Result){
if (Result != NULL){
printf("%d\n", Result->data);
}
else{
printf("Not Found: %d\n", SearchTarget);
}
}
int main(){
BSTNode* Tree = BST_CreateNode(123);
BSTNode* Node = NULL;
BST_InsertNode(Tree, BST_CreateNode(22));
BST_InsertNode(Tree, BST_CreateNode(9918));
BST_InsertNode(Tree, BST_CreateNode(424));
BST_InsertNode(Tree, BST_CreateNode(17));
BST_InsertNode(Tree, BST_CreateNode(3));
BST_InsertNode(Tree, BST_CreateNode(98));
BST_InsertNode(Tree, BST_CreateNode(34));
BST_InsertNode(Tree, BST_CreateNode(760));
BST_InsertNode(Tree, BST_CreateNode(317));
BST_InsertNode(Tree, BST_CreateNode(1));
int searchTarget = 30;
Node = BST_SearchNode(Tree, searchTarget);
PrintSearchResult(searchTarget, Node);
return 0;
}
실행 결과
Not Found: 30


댓글남기기