sk-choi

This is the place that record about something today I learned.

Intro

이 글에서는 정렬 알고리즘의 버블 정렬, 선택 정렬과 삽입 정렬에 대해서 다룹니다.

정렬 알고리즘이란?

정렬 알고리즘은 정해진 기준에 따라 데이터를 순서대로, 체계적으로 정리하는 알고리즘이다.

상품을 가격별로 오름차순/내림차순으로 정렬할 때나 시험에서의 응시생 점수를 정렬 할 때 이러한 정렬 알고리즘이 사용된다.

정렬의 제일 큰 목적은 무언가를 탐색하는 데에 필요한 밑바탕을 만드는 것이다.

즉 탐색에 용이한 환경을 만드는 것에 정렬 알고리즘이 활용되고, 이러한 정렬 과정을 통해 탐색을 좀 더 효율적으로 진행할 수 있다.

이 글에서는 정렬 알고리즘의 종류 중에서 버블 정렬, 선택 정렬, 삽입 정렬에 대해서 다룰 것이다.

Unstable sort vs Stable sort

알고리즘을 수행할 때 동일한 값을 가지는 원소들의 본래 순서가 보장될 때 Stable sort(안정 정렬)이라 한다.

안정 정렬 종류: 삽입 정렬, 버블 정렬, 병합 정렬

반대로 동일한 값을 가지는 원소들의 본래 순서가 보장되지 않으면 Unstable sort(불안정 정렬)이라고 한다.

불안정 정렬 종류: 선택 정렬, 퀵 정렬, 힙 정렬, 인트로 정렬(퀵 정렬+힙 정렬)

In-place sort 

기존 배열 외의 추가적인 메모리를 거의 사용하지 않는다면 제자리 정렬(In-place sort)이라고 한다.

장점: 기존 배열 외의 추가적인 공간을 필요로 하지 않기 때문에, 공간 복잡도가 낮다.

종류: 삽입 정렬, 선택 정렬, 버블 정렬, 퀵 정렬, 힙 정렬

버블 정렬 알고리즘 개념

img

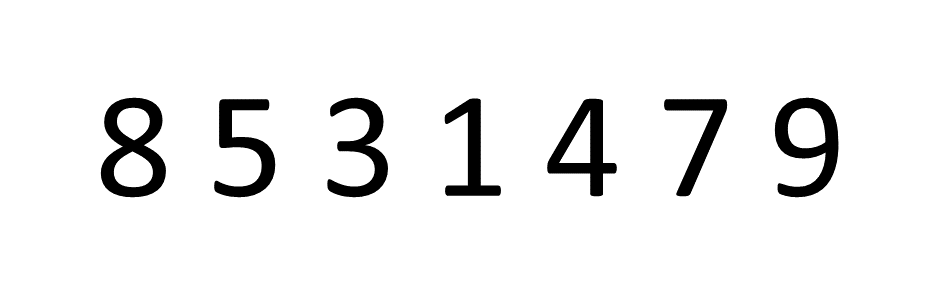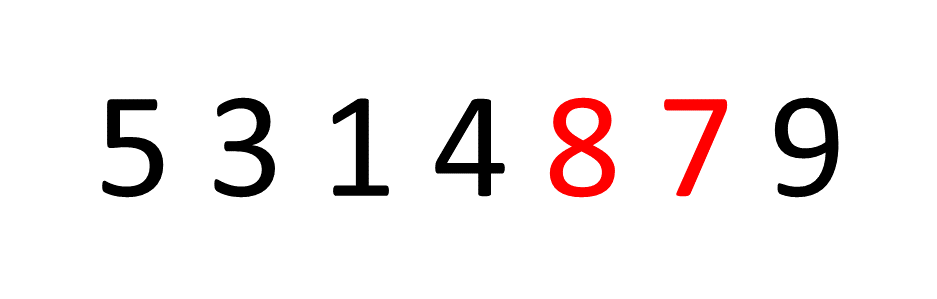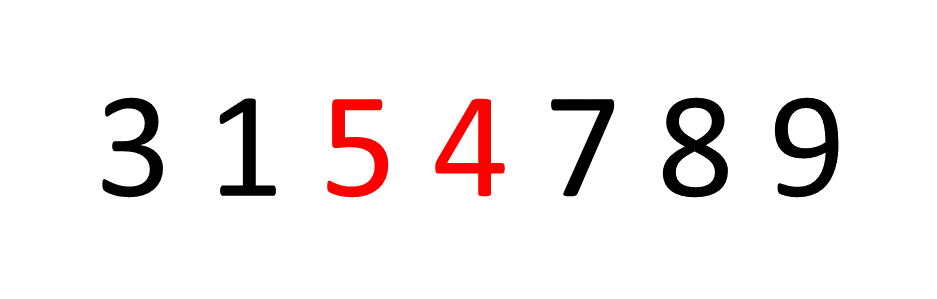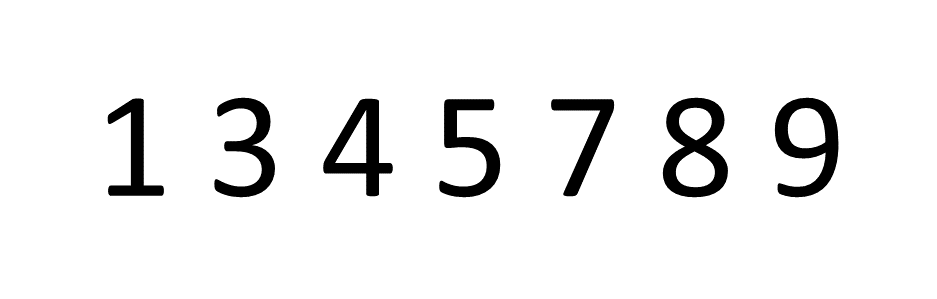
버블이란 이름은 물 속 깊은 곳에서 거품이 수면을 향해 올라오는 것처럼 자료를 정렬해서 붙여진 이름이다.

버블 정렬은 이웃끼리 데이터를 교환하면서 정렬을 진행한다.

즉, 이중 반복문 안에서 안쪽의 반복문을 수행할 때 모든 이웃끼리 원소를 비교하면서 하나씩 정렬을 시도한다.

ex. 5,1,6,4,2,3

->156423

->154623

->154263

->154236 (1차 완료)…

시간 복잡도: (n-1)+(n-2)+(n-3)+…+1 = n(n-1)/2 = O(n2)

버블 정렬 알고리즘 구현 코드

#include <stdio.h>

void bubblesortion(int data[], int length){
    int i = 0;
    int j = 0;
    int temp = 0;
    
    for (i = 0; i < length; i++){
        for (j = 0; j < length-1; j++){
            if(data[j] > data[j+1]){ //data[j]가 data[j+1]보다 크면 서로 체인지
                temp = data[j+1];
                data[j+1] = data[j];
                data[j] = temp;
            }
        }
    }
}

int main(void){
    int data[] = {6,4,2,3,1,5};
    int length = sizeof(data)/sizeof(data[0]);
    int i = 0;
    
    bubblesortion(data, length);
    
    for(i = 0; i < length; i++){
        printf("%d", data[i]);
    }
    printf("\n");
    
    return 0;
}

선택 정렬 알고리즘 개념

img
선택 정렬은  정렬되지 않은 데이터 중에서 가장 작은 데이터를 찾아 가장 앞의 데이터와 교환하면서 정렬을 진행하는 방식이다.

시간 복잡도: (n-1)+(n-2)+(n-3)+…+1 = n(n-1)/2 = O(n2)

선택 정렬 알고리즘 구현 코드

#include <stdio.h>

void selectionsortion(int data[], int length){
    int i = 0;
    int j = 0;
    int temp = 0;
    
    for (i = 0; i < length-1; i++){
       for (j = i+1; j < length; j++){
           if (data[i] > data[j]){
               temp = data[i];
               data[i] = data[j];
               data[j] = temp;
           }
       } 
    }
}

int main(void){
    int data[] = {6,4,2,3,1,5};
    int length = sizeof(data)/sizeof(data[0]);
    int i = 0;
    
    selectionsortion(data, length);
    
    for(i = 0; i < length; i++){
        printf("%d", data[i]);
    }
    printf("\n");
    
    return 0;
}

삽입 정렬 알고리즘 개념

img

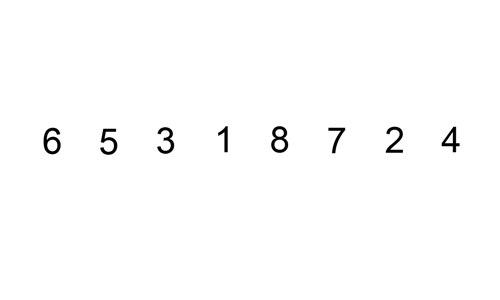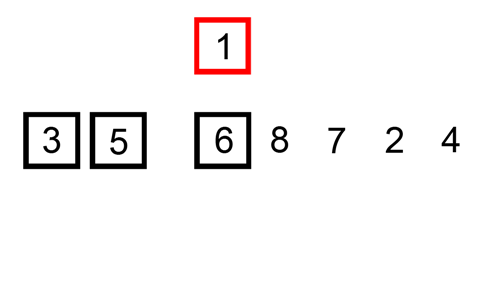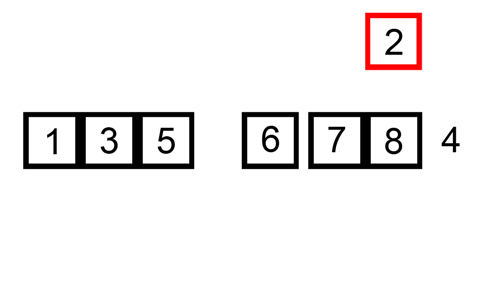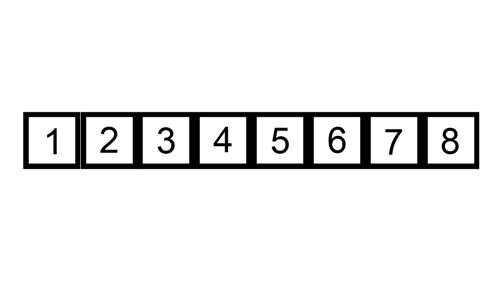
삽입정렬은 자료구조를 순차적으로 순회하면서 순서에 어긋나는 요소를 찾고, 그 요소를 올바른 위치에 다시 삽입해나가는 정렬 알고리즘이다.

ex. 54321

i = 1
vl = 4;

55321
45321

i = 2
vl = 3
44521
34521

i = 3
vl = 2
33451
23451

i = 4
vl = 1
22345
12345

시간 복잡도

최선의 경우: O(n) -> 자료구조가 이미 정렬되어 있다면 한 번도 비교를 거치지 않기 때문이다.

최악의 경우: (n-1)+(n-2)+(n-3)+…+1 = n(n-1)/2 = O(n2)

삽입 정렬 알고리즘 구현 코드

삽입 정렬 알고리즘은 c언어의 memmove 함수를 이용해서 구현이 가능하다.

memmove함수는 memmove(dest, src, size)의 구조로 이루어져 있으며, src의 size크기만큼 dest에 붙여넣는 기능을 수행한다.

여기서는 memmove를 사용 안 한 것과 사용한 버전 두 가지를 보여주고자 한다.

일반 구현 코드

#include <stdio.h>

void insertionsort(int data[], int length){
    int i = 0;
    int j = 0;
    int value = 0;
    
    for (i = 1; i < length; i++){
        value = data[i];
        for (j = i - 1; j >= 0 && data[j] > value; j--){
            data[j+1] = data[j];
        }
        data[j+1] = value;
    }
}

int main(void){
    int data[] = {6,4,2,3,1,5};
    int length = sizeof(data)/sizeof(data[0]);
    int i;
    
    insertionsort(data, length);
    
    for(i = 0; i < length; i++){
        printf("%d", data[i]);
    }
    printf("\n");
    
    return 0;
}

memmove사용한 구현 코드

#include <stdio.h>
#include <string.h>

void insertionsort(int data[], int length){
    int i = 0;
    int j = 0;
    int value = 0;
    
    for (i = 1; i < length; i++){
        if(data[i-1] <= data[i]){
            continue;
        }
        
        value = data[i];
        
        for (j = 0; j < i; j++){
            if (data[j] > value){
                memmove(&data[j+1], &data[j], sizeof(data[0])*(i-j));
                data[j] = value;
                break;
            }
        }
    }
}

참고