sk-choi

This is the place that record about something today I learned.

Intro

이 글은 이진 트리(Binary Tree) 자료 구조의 개념과 특징, 그리고 구현에 대한 정보를 담은 글입니다.

이진 트리 개념 및 특징

 

이진 트리 개념: 하나의 노드가 자식 노드를 두 개 까지만 가질 수 있는 트리 구조

이진 트리는 컴파일러나 검색과 같은 알고리즘의 뼈대가 되는 특별한 자료구조이다. 특히 완전한 이진 트리에서는 높은 검색 성능을 낼 수 있다.

img

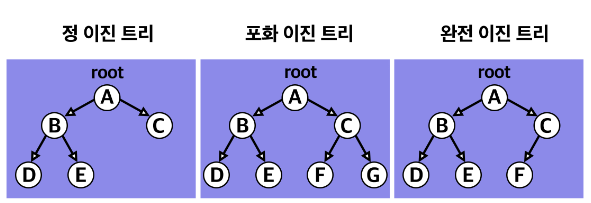
포화 이진 트리 : 잎 노드를 제외한 모든 노드가 자식 노드를 두 개씩 가진 이진 트리

완전 이진 트리: 포화 이진 트리의 전 단계로, 잎 노드가 트리 왼쪽부터 차곡차곡 채워진 트리

img

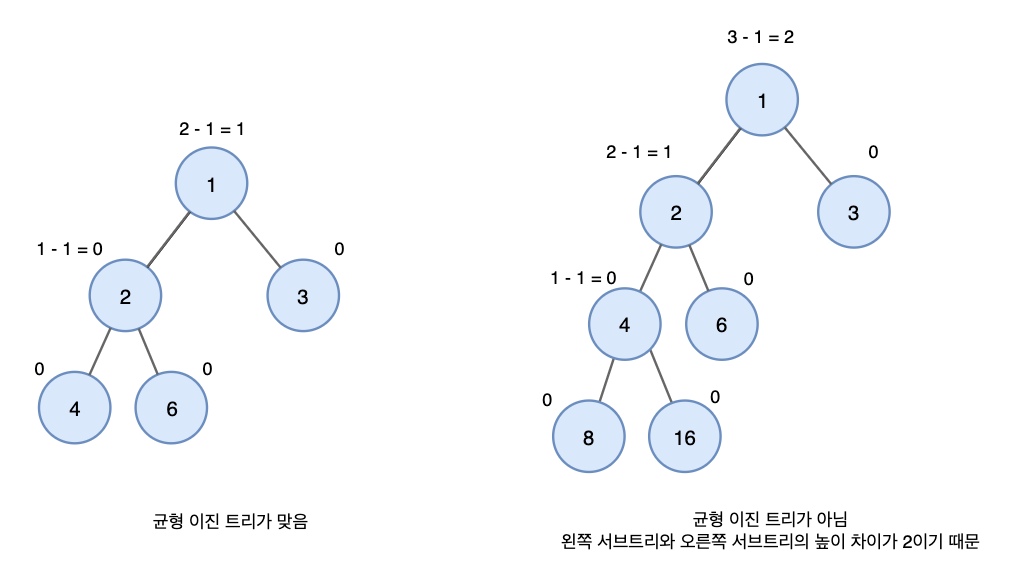
높이 균형 트리 : 뿌리 노드를 기준으로 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 2 이상 차이 나지 않는 이진 트리

완전 높이 균형 트리 : 뿌리 노드를 기준으로 왼쪽 하위 트리와 오른쪽 하위 트리의 높이가 같은 이진 트리

순회 방법

순회: 트리 안에서 노드 사이를 이동하는 연산을 말함. 그리고 이러한 순회는 데이터 접근 순서에 따라 전위, 중위, 후위 순회로 분류된다.

img

전위 순회 : 뿌리 노드부터 잎 노드까지 아래 방향으로 내려오면서 왼쪽 하위 트리를 방문하고 왼쪽 하위 트리의 방문이 끝나면 오른쪽 하위 트리를 방문하는 방식. 위의 그림을 예시로 보자면, A->B->D->E->C->F->G 순서로 노드 방문을 하게 된다.

중위 순회 : 왼쪽 하위 트리부터 시작해서 뿌리 노드를 거쳐 오른쪽 하위 트리를 방문하는 순회 방법.

위의 그림을 예시로 보자면, D->B->E->A->F->C->G 순서로 노드 방문을 한다.

후위 순회 : 왼쪽 하위 트리부터 시작해서 오른쪽 하위 트리를 거쳐 뿌리 노드를 방문하는 순회 방법.

위의 그림을 예시로 보자면, D->E->B->F->G->C->A 순서로 노드 방문을 한다.

코드 구현

완전 이진트리의 코드 구현은 백준 사이트의 1991번 문제인 트리 순회로 대신한다.

코드는 다음과 같다.

#include <stdio.h>
#include <stdlib.h>

typedef struct tagBTNode
{
    struct tagBTNode* left;
    struct tagBTNode* right;
    
    char data;
}BTNode;

BTNode* createNode(char newdata){
        
    BTNode* NewNode = (BTNode*)malloc(sizeof(BTNode));
    NewNode->left = NULL;
    NewNode->right = NULL;
    NewNode->data = newdata;
    
    return NewNode;
}

/* 원래 내가 작성한 함수:
BTNode* findNode(BTNode* Root, char finddata){
    
    if (Root->data == finddata){
        return Root;
    }
    else{
        return NULL;
    }
    findNode(Root->left, finddata);
    findNode(Root->right, finddata);
}
*/

// 새로 작성한 findNode 함수
BTNode* findNode(BTNode* Root, char finddata){ //findNode 함수의 논리적 오류 때문에 다시 수정!!
    
    if (Root == NULL){
        return NULL;
    }
    
    if (Root->data == finddata){
        return Root;
    }
    BTNode* foundNode = findNode(Root->left, finddata);
    if (foundNode == NULL){
        foundNode = findNode(Root->right, finddata);
    }
    return foundNode;
}

void destroyNode(BTNode* Node){
    free(Node);
}

/*원래 작성했던 addchild함수
void addchild(BTNode* Node, BTNode* Child) {
    if (Node->left == NULL) {
        Node->left = Child;
    }
    else {
        Node->right = Child;
    }
}
*/

void printpreorder(BTNode* Node){
    if (Node == NULL){
        return;
    }
        printf("%c", Node->data);
        printpreorder(Node->left);
        printpreorder(Node->right);
}

void printinorder(BTNode* Node){
    if (Node == NULL){
        return;
    }
    printinorder(Node->left);
    printf("%c", Node->data);
    printinorder(Node->right);
}

void printpostorder(BTNode* Node){
     if (Node == NULL){
        return;
    }
    printpostorder(Node->left);
    printpostorder(Node->right);
    printf("%c", Node->data);
    
}

void destroyTree(BTNode* Node){
    
    if (Node == NULL){
        return;
    }
    destroyTree(Node->left);
    destroyTree(Node->right);
    destroyNode(Node);
}

// 처음에 addchild함수로 left가 없으면 left, left가 있으면 right에 넣는 방식으로 자식 노드를 추가했지만
// 문제에서 요구하는 건 두 번째로 입력한 원소가 left, 세 번째로 입력한 원소가 right로 들어가는 것이므로
// 코드를 문제의 요구 사항에 맞게 수정했다.
int main(void){
    int N;
    scanf("%d", &N);
    
    BTNode* Node = NULL;

    while(N > 0){
        char a, b, c;
        scanf(" %c %c %c", &a, &b, &c);
        
        if (Node == NULL){
            Node = createNode(a);   
            if(b != '.'){
                BTNode* Node2 = createNode(b);
                Node->left = Node2;
            }                
            if(c != '.'){
                BTNode* Node3 = createNode(c);
                Node->right = Node3;
            }
        }
        else{
            BTNode* Node1 = findNode(Node, a);
            if(Node1 != NULL){
                if (b != '.'){
                    BTNode* Node2 = createNode(b);
                    Node1->left = Node2;
                }
                if (c != '.'){
                    BTNode* Node3 = createNode(c);
                    Node1->right = Node3;
                }
            }
        }
        N--;
    }
    
    printpreorder(Node);
    printf("\n");
    printinorder(Node);
    printf("\n");
    printpostorder(Node);
    
    destroyTree(Node);
}

참고